Вычислительная стратегия программирования в ограничениях

В основе предлагаемой вычислительной стратегии разрешения ограничений лежит несколько конструктивных принципов и идей:

использование единого метамодельного представления для работы с данными и моделями, специфицированными на языках EXPRESS, ODL/OQL, UML/OCL, OWL; для взаимного преобразования моделей и определяемых ими данных могут быть применены известные трансформации;

статический анализ спецификаций модели данных и идентификация математических постановок, к которым может быть сведена исходная задача в ограничениях; для простых ограничений формируются альтернативные правила пересчета неизвестных переменных друг через друга, пригодные для использования в методах распространения; для сложных систем ограничений (и их подсистем) осуществляется анализ зависимостей по данным и определяется тип математической задачи, а также возможный метод решения (например, идентификация множества ограничений как системы линейных алгебраических уравнений позволяет использовать известные методы матричной факторизации);

последовательная редукция исходной задачи в ограничениях к задачам формирования множества неизвестных переменных (расчет необходимого числа объектов каждого типа), установления взаимосвязей (отношений ассоциации, агрегации и композиции между объектами) и определения числовых параметров (значений атрибутов объектов);

применение методов линейного и квадратичного целочисленного программирования для определения кардинальности множеств типизированных объектов; выбор вида функционала позволяет эмулировать содержательные ситуации, когда, например, требуется сформировать минимальные, максимальные или репрезентативные наборы данных;

применение методов логического вывода (прежде всего, метода резольвент и метода полисиллогистического вывода) для задания взаимосвязей объектов и определения неизвестных логического типа;

применение методов интервальной арифметики, локализации и распространения для нахождения неизвестных вещественного типа при наличии простых зависимостей по данным;

применение известных методов символьных преобразований и вычислительной математики для совместного решения систем (линейных, полиномиальных, нелинейных) алгебраических уравнений и неравенств;

применение метода семантической реконсиляции для инкрементального поиска общих решений с учетом всей системы наложенных разнородных ограничений.

Таким образом, в качестве основной стратегии предлагается использовать описанную выше редукционную схему, состоящую в последовательном конструировании необходимого числа типизированных объектов, задании для них взаимосвязей и определении значений их атрибутов. Заметим, что большая часть семантических правил в объектно-ориентированных моделях специфицируется независимым друг от друга образом и не приводит к сложным зависимостям по данным. Это дает основания полагать о конструктивности применения подобной стратегии.

В более сложных ситуациях, когда основная стратегия не обеспечивает нахождение общего решения, предлагается использовать оригинальный метод семантической реконсиляции для коррекции уже найденных частных решений. Ключевые элементы этого метода были успешно апробированы в приложениях коллективной инженерии, к которым предъявляются близкие требования целостности и корректности результирующего представления данных. Применительно к обсуждаемому классу задач CLP(O) метод семантической реконсиляции предполагает следующие этапы:

валидация семантических правил модели для исходных объектно-ориентированных данных и идентификация ограничений, не разрешенных в результате применения редукционного подхода;

определение альтернативных способов коррекции для каждого нарушенного правила (определение наборов элементарных операций над множествами объектов, исправляющих нарушенные правила);

совместный анализ выявленных способов коррекции с учетом уже выполненных правил и установление логических отношений между элементарными операциями;

формирование и решение разреженной системы логических уравнений, и определение допустимых комбинаций элементарных операций, удовлетворяющих всем ограничениям модели;

коррекция исходных данных путем применения вычисленных наборов операций.

Ожидается, что применение редукционного подхода в сочетании с методом семантической реконсиляции обеспечит надежное решение задач в классе CLP(O).

Проиллюстрируем применение описанной вычислительной стратегии на примере задачи о правильном многограннике. Задача формулируется следующим образом: в трехмерном пространстве требуется построить правильный многогранник с заданным числом граней. Отметим, что в подобной постановке решение может и не существовать (известным фактом, например, является невозможность построения правильного пятигранника), поэтому желателен анализ существования решения.

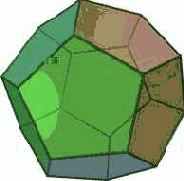
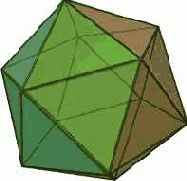
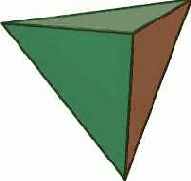
Вычислительная стратегия программирования в ограничениях

Рис. 5. Додекаэдр, икосаэдр, тетраэдр

Опишем задачу в ограничениях в виде спецификаций модели данных. Определим абстрактный класс polyhedron для представления произвольного правильного многогранника. Многогранник состоит из граней, ребер и вершин, моделируемых классами face, edge и vertex соответственно. Конкретизации класса polyhedron (см. рис. 5), соответствующие геометрическим моделям:

тетраэдра – имеет 4 треугольных грани, 6 рёбер, 4 вершины, в каждой сходятся 3 ребра,
октаэдра – имеет 8 треугольных граней, 8 ребер, 6 вершин, в каждой сходятся 4 ребра,
гексаэдра – имеет 6 четырехугольных граней, 12 ребер, 8 вершин, в каждой сходятся 4 ребра,
додекаэдра – имеет 12 пятиугольных граней, 30 рёбер и 20 вершин, в каждой сходятся 3 ребра и
икосаэдра – имеет 20 треугольных граней, 30 рёбер, 12 вершин, в каждой сходятся 5 ребер,

моделируются классами tetrahedron, octahedron, hexahedron, dodecahedron и icosahedron соответственно. В рассматриваемой постановке абсолютный масштаб многогранника не существенен, поэтому для определенности положим длину ребер равной единице.

На рис. 6 приведена диаграмма классов UML, определяющая основные типы данных для представления многогранников. Условия исходной задачи редуцированы в ограничения кратности для отношений ассоциаций и агрегаций между классами модели данных.

Однако для исчерпывающей постановки исходной задачи требуется также задать:

условие согласованности и связности топологических элементов многогранника, определяемое, в частности, формулой Эйлера для общего числа вершин, ребер и граней;
условие выпуклости многогранника, например, в виде правил пространственной локализации его вершин в полупространствах, задаваемых плоскостями граней;
условие правильности многогранника как равенства длин всех его ребер выбранному единичному значению.

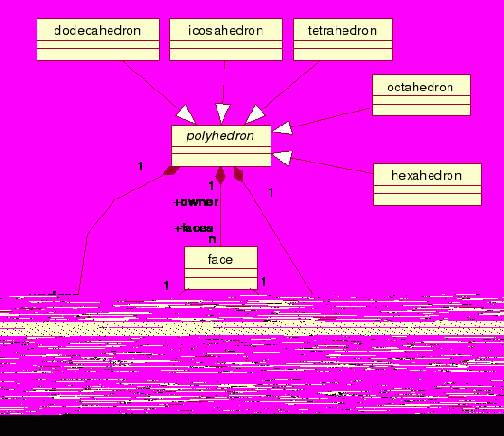
Рис. 6. UML модель для представления многогранников

Для описания этих ограничений воспользуемся языком OCL. Формула Эйлера для многогранника представляется в виде следующего инварианта, распространяемого на экземпляры класса polyhedron:

context polyhedron inv: self.vertices->size() - self.edges->size() + self.faces->size() = 2

Для задания ограничения выпуклости воспользуемся уравнением плоскости , проходящей через первые три вершины каждой грани и задающей полупространство для локализации остальных вершин многогранника. На языке OCL условие выпуклости многогранника может быть выражено соответствующим инвариантом класса face, в котором используются объявления вспомогательных локальных переменных:

context face let secVertices : Sequence(Vertex) = collect(self.v) in let first : Vertex = secVertices(1) in let second : Vertex = secVertices(2) in let third : Vertex = secVertices(3) in

let A : Real = first.y * (second.z - third.z ) + second.y * (third.z - first.z ) + third.y * (first.z - second.z ) in let B : Real = first.z * (second.x - third.x ) + second.z * (third.x - first.x ) + third.z * (first.x - second.x ) in

let C : Real = first.x * (second.y - third.y ) + second.x * (third.y - first.y ) + third.x * (first.y - second.y ) in

let D : Real = first.x * (third.y * second.z - second.y * third.z) + second.x * (first.y * third.z - third.y * first.z) + third.x * (second.y * first.z - first.y * second.z) in

self.owner.vertices->collect( v1 : vertex | not self.vertices->includes( v1 ) ) ->forAll( v2 : vertex | A * v2.x + B * v2.y + C * v2.z + D > 0 )

Наконец, условие равенства длин ребер прозрачным образом специфицируется средствами языка OCL как инвариант класса edge:

Context edge inv: (self.v2.x – self.v1.x) * (self.v2.x – self.v1.x) + (self.v2.y – self.v1.y) * (self.v2.y – self.v1.y) + (self.v2.z – self.v1.z) * (self.v2.z – self.v1.z) = 1

В рамках описанной выше общей вычислительной стратегии программирования в ограничениях правильный многогранник может быть построен путем последовательной редукции исходной задачи к типовым математическим постановкам и их согласованного решения. При использовании данной стратегии, сначала проводится идентификации и разрешение ограничений связанных с количеством топологических элементов многогранника. Как результат, определяется требуемое количество объектов соответствующих типов UML модели, а из их атрибутов формируется вектор неизвестных переменных.

Затем на основе анализа спецификаций ограничений формируется система нелинейных алгебраических уравнений и неравенств относительно переменных, соответствующих координатам вершин многогранника. Решение системы может быть осуществлено численным образом, например, с использованием квази-ньютоновских методов, хорошо зарекомендовавших себя при решении широких классов нелинейных алгебраических задач.

Рассмотренный пример иллюстрирует возможность применения единой стратегии для решения довольно сложных вычислительных задач, в постановке которых участвуют разнородные ограничения.

Содержание раздела

Главная сайта